Pembuktian Rumus Jari-Jari Bulat Dalam Dan Luar Segitiga Serta Bulat Singgung Segitiga
Dari sebuah segitiga, kita sanggup membuat bundar baik itu dalam segitiga maupun luar segitiga. Dimana pada bundar dalam segitiga, bundar menyinggung ketiga sisi segitiga dari dalam. Sedangkan pada bundar luar segitiga, bundar menyinggung ketiga titik sudut segitiga. Artikel kali ini, akan mengulas terkena pembuktian rumus jari-jari bundar dalam segitiga, jari-jari bundar luar segitiga dan jari-jari bundar singgung segitiga yang disertai uraian penurunannya atau pembuktiannya.
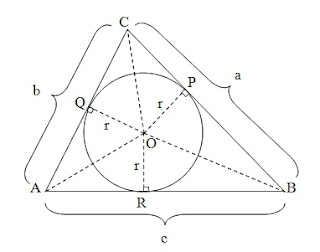
Segitiga ABC di atas ialah segitiga sebarang. Titik P, Q, dan R ialah titik singgung antara segitiga ABC dengan bundar yang berpusat di O. OP = OQ = OR = r yang ialah jari-jari dari bundar O. Panjang BC = a, AC = b, dan AB = c. Dari titik A, B, C, dan O terbentuk 3 buah segitiga yaitu segitiga AOB, segitiga AOC, dan segitiga BOC dengan tinggi sama yaitu r. Luas dari masing-masing segitiga tersebut adalah
Luas Segitiga AOB = 1/2 x AB x OR
Luas Segitiga AOC = 1/2 x AC x OQ
Luas Segitiga BOC = 1/2 x BC x OP
Untuk memilih jari-jari bundar dalam segitiga AOB kita sanggup memakai persamaan bahwa Luas Segitiga ABC sama dengan jumlah Luas Segitiga AOB, Luas Segitiga AOC dan Luas Segiitiga BOC atau sanggup ditulis sebagai diberikut

Jadi, rumus jari-jari bundar dalam suatu segitiga adalah

melaluiataubersamaini s = setengah keliling atau s = ½ (a + b + c) dan L = luas segitiga. Luas segitiga sanggup ditentukan dua cara yaitu
L = ½ x Alas x Tinggi
Rumus di atas sanggup dipakai apabila ganjal dan tinggi segitiga sanggup ditentukan dengan jelas. Bila tidak, maka luas segitiga juga sanggup ditentukan dengan formula Heron yaitu

Dari gambar segitiga ABC di atas, diperoleh juga rumus jarak titik sudut segitiga terhadap titik singgung dengan lingkarannya.
Misalkan panjang AR = AQ = x, BR = BP = y, dan CP =CQ = z. Sehingga
AR + BR = AB atau x + y = c
BP + CP = BC atau y + z = a
AQ + CQ = AC atau x + z = b
Rumus Jari-Jari Lingkaran Dalam Segitiga
Perhatikan gambar segitiga di bawah ini!Segitiga ABC di atas ialah segitiga sebarang. Titik P, Q, dan R ialah titik singgung antara segitiga ABC dengan bundar yang berpusat di O. OP = OQ = OR = r yang ialah jari-jari dari bundar O. Panjang BC = a, AC = b, dan AB = c. Dari titik A, B, C, dan O terbentuk 3 buah segitiga yaitu segitiga AOB, segitiga AOC, dan segitiga BOC dengan tinggi sama yaitu r. Luas dari masing-masing segitiga tersebut adalah
Luas Segitiga AOB = 1/2 x AB x OR
Luas Segitiga AOC = 1/2 x AC x OQ
Luas Segitiga BOC = 1/2 x BC x OP
Untuk memilih jari-jari bundar dalam segitiga AOB kita sanggup memakai persamaan bahwa Luas Segitiga ABC sama dengan jumlah Luas Segitiga AOB, Luas Segitiga AOC dan Luas Segiitiga BOC atau sanggup ditulis sebagai diberikut

Jadi, rumus jari-jari bundar dalam suatu segitiga adalah

melaluiataubersamaini s = setengah keliling atau s = ½ (a + b + c) dan L = luas segitiga. Luas segitiga sanggup ditentukan dua cara yaitu
L = ½ x Alas x Tinggi
Rumus di atas sanggup dipakai apabila ganjal dan tinggi segitiga sanggup ditentukan dengan jelas. Bila tidak, maka luas segitiga juga sanggup ditentukan dengan formula Heron yaitu

Dari gambar segitiga ABC di atas, diperoleh juga rumus jarak titik sudut segitiga terhadap titik singgung dengan lingkarannya.
Misalkan panjang AR = AQ = x, BR = BP = y, dan CP =CQ = z. Sehingga
AR + BR = AB atau x + y = c
BP + CP = BC atau y + z = a
AQ + CQ = AC atau x + z = b
Jadi,
x = s – (y + z) = s – a
y = s – (x + z) = s – b
z = s – (x + y) = s – c
atau
AR = AQ = s – a
BR = BP = s – b
CP = CQ = s – c
Rumus Jari-Jari Lingkaran Luar Segitiga
Lingkaran luar segitiga ialah bundar yang terbentuk melalui ketiga titik sudut suatu segitiga. jikalau digambarkan maka di dalam bundar terdapat sebuah segitiga yang titik-titik sudutnya dilalui oleh lingkaran. Misalkan, terdapat segitiga sebarang ABC dengan panjang sisi-sisi dihadapan sudut A= a, sudut B = b, dan C = c. Lingkaran O ialah bundar yang melalui ketiga titik sudut segitiga ABC, sehingga segitiga ABC berada di dalam bundar O. Untuk lebih jelasnya diberikut yaitu ilustrasinya
Selanjutnya, CD ialah garis tinggi dari segitiga ABC dan Garis CE ialah diameter bundar (d = 2r). Segitiga ACE sebangun dengan segitiga BCD. Hal ini sebab sudut BDC sama dengan sudut CAE = 90o (Sudut CAerupakan sudut keliling yang menghadap diameter), sudut AEC sama dengan sudut CBD sebab kedua sudut menghadap busur yang sama, sehingga ACE juga sama dengan sudut BCD. Ini berarti sanggup disimpulkan keduanya sebangun. Dari kesebangunan tersebut diperoleh bahwa
Secara umum, sebab ½ x CD x AB yaitu luas segitiga ABC maka secara umum rumus jari-jari bundar luar segitiga adalah
melaluiataubersamaini a, b, c yaitu panjang sisi-sisi dari segitiga dan L yaitu luas segitiga yang sanggup ditentukan dengan
L = ½ x ganjal x tinggi
atau
Rumus Lingkaran Singgung Segitiga
Lingkaran singgung segitiga sendiri ialah bundar yang menyinggung salah satu sisi suatu segitiga dari luar serta menyinggung perpantidakboleh dari sisi-sisi yang lain dari segitiga tersebut. Berikut ini saya akan coba menguraikan penurunan rumus jari-jari bundar singgung segitiga.
Perhatikan gambar segitiga ABC di bawah
Misalkan dibentuk bundar yang menyinggung sisi a, maka bundar singgung segitiga tersebut sanggup digambarkan melalui gambar diberikut.
Dari gambar terlihat bahwa, bundar singgung berpusat di O dengan menyinggung sisi a serta menyinggung perpantidakboleh dari sisi b dan c. Jari-jari bundar singgung segitiga yang menyinggung sisi a disebut dengan ra . ODAE, ODCF, dan OFBE ialah layang-layang garis singgung. Panjang EB = FB = p, DC = FC = (a - p), serta panjang OD = OF = OE = ra . Untuk memilih panjang OA sanggup dilakukan dengan dua cara yaitu
OA2 = AD2 + OD2 .......1)
OA2 = AE2 + OE2 ........2)
Dari 1) dan 2) diperoleh

Untuk memilih luas layang-layang garis singgung ODAE sanggup dilakukan dengan dua cara yaitu
Luas ODAE = 2 x L. Segitiga OEA
Luas ODAE = 2 x ½ x OE x EA
Luas ODAE = OE x EA
Luas ODAE = ra x (c + p)
Luas ODAE = ra x (c + s – c)
Luas ODAE = ra x s ....................3)
Luas ODAE = Luas Segitiga ABC + Luas ODCF + Luas OEBF
Luas ODAE = Luas Segitiga ABC + 2 x Luas Segitiga ODC + 2 x Luas Segitiga OEB
Luas ODAE = Luas Segitiga ABC + 2 x ½ x OE x EB + 2 x ½ x OD x DC
Luas ODAE = Luas Segitiga ABC + OE x EB + OD x DC
Luas ODAE = Luas Segitiga ABC + ra x p + ra x (a – p)
Luas ODAE = luas Segitiga ABC + ra x (p + a – p)
Luas ODAE = Luas Segitiga ABC + ra x a ..................4)
Dari 3) dan 4) diperoleh

Sehingga, secara umum rumus jari-jari bundar singgung segitiga yang menyinggung sisi a sanggup ditetapkan dengan

Dimana, s ialah setengah keliling segitiga atau s = ½ (a + b + c) dan L ialah luas segitiga yang sanggup dicari dengan dua cara yaitu setengah dikali panjang ganjal dikali tinggi (L = ½ x ganjal x tinggi) atau dengan memakai formula Heron yaitu

melaluiataubersamaini cara yang sama pula, kita akan mendapat rumus jari-jari bundar singgung yang menyinggung sisi b dan sisi c. Sehingga, secara lengkap rumus jari-jari bundar segitiga sanggup ditetapkan sebagai diberikut.

Untuk pola soal, jari-jari bundar dalam dan luar segitiga sanggup dilihat pada artikel ini
Perhatikan gambar segitiga ABC di bawah
Misalkan dibentuk bundar yang menyinggung sisi a, maka bundar singgung segitiga tersebut sanggup digambarkan melalui gambar diberikut.
Dari gambar terlihat bahwa, bundar singgung berpusat di O dengan menyinggung sisi a serta menyinggung perpantidakboleh dari sisi b dan c. Jari-jari bundar singgung segitiga yang menyinggung sisi a disebut dengan ra . ODAE, ODCF, dan OFBE ialah layang-layang garis singgung. Panjang EB = FB = p, DC = FC = (a - p), serta panjang OD = OF = OE = ra . Untuk memilih panjang OA sanggup dilakukan dengan dua cara yaitu
OA2 = AD2 + OD2 .......1)
OA2 = AE2 + OE2 ........2)
Dari 1) dan 2) diperoleh

Untuk memilih luas layang-layang garis singgung ODAE sanggup dilakukan dengan dua cara yaitu
Luas ODAE = 2 x L. Segitiga OEA
Luas ODAE = 2 x ½ x OE x EA
Luas ODAE = OE x EA
Luas ODAE = ra x (c + p)
Luas ODAE = ra x (c + s – c)
Luas ODAE = ra x s ....................3)
Luas ODAE = Luas Segitiga ABC + Luas ODCF + Luas OEBF
Luas ODAE = Luas Segitiga ABC + 2 x Luas Segitiga ODC + 2 x Luas Segitiga OEB
Luas ODAE = Luas Segitiga ABC + 2 x ½ x OE x EB + 2 x ½ x OD x DC
Luas ODAE = Luas Segitiga ABC + OE x EB + OD x DC
Luas ODAE = Luas Segitiga ABC + ra x p + ra x (a – p)
Luas ODAE = luas Segitiga ABC + ra x (p + a – p)
Luas ODAE = Luas Segitiga ABC + ra x a ..................4)
Dari 3) dan 4) diperoleh

Sehingga, secara umum rumus jari-jari bundar singgung segitiga yang menyinggung sisi a sanggup ditetapkan dengan

Dimana, s ialah setengah keliling segitiga atau s = ½ (a + b + c) dan L ialah luas segitiga yang sanggup dicari dengan dua cara yaitu setengah dikali panjang ganjal dikali tinggi (L = ½ x ganjal x tinggi) atau dengan memakai formula Heron yaitu

melaluiataubersamaini cara yang sama pula, kita akan mendapat rumus jari-jari bundar singgung yang menyinggung sisi b dan sisi c. Sehingga, secara lengkap rumus jari-jari bundar segitiga sanggup ditetapkan sebagai diberikut.

Untuk pola soal, jari-jari bundar dalam dan luar segitiga sanggup dilihat pada artikel ini








0 Response to "Pembuktian Rumus Jari-Jari Bulat Dalam Dan Luar Segitiga Serta Bulat Singgung Segitiga"
Posting Komentar