Pembagian Suku Banyak Dan Referensi Soalnya
Dalam bahasan kali ini, kita akan mengulas terkena proteksi suku banyak. Dalam hal ini, proteksi suku banyak yang akan dibahas kita batasi dari segi pembaginya yaitu, proteksi suku banyak dengan (x – k), (ax + b), dan (ax2 + bx + c)
f(x) = P(x) H(x) + S
atau
f(x) = (x – k) H(x) + S
Dimana f(x) ialah suku banyak, (x – k) ialah pembaginya, H(x) ialah hasil baginya, dan S ialah sisa pertolongannya. Oleh alasannya pembagi P(x) = x – k berderajat satu, maka sisa S maksimum berderajat nol atau berupa suatu konstanta yang tidak memuat variabel. Dari bentuk di atas kita akan mendapat Teorema Sisa 1 diberikut
Teorema Sisa 1
Jika suku banyak f(x) dibagi (x – k), maka sisa pertolongannya ialah S = f(k)
Bukti:
f(x) = (x – k) H(x) + S
f(k) = (k – k) H(x) + S
f(k) = 0 H(x) + S
f(k) = S
Jadi, terbukti S = f(k)
melaluiataubersamaini kata lain kita akan mendapat sisa dari suatu proteksi f(x) dengan pembagi (x – k) dengan mensubstitusi k ke suku banyak f(x)
Untuk memilih hasil bagi dan sekaligus sisa proteksi dari suatu suku banyak kita sanggup memakai dua cara yaitu cara proteksi biasa (cara bersusun) dan cara skema atau horner/skema. Untuk lebih jelasnya perhatikan pola soal diberikut
misal 1
Tentukanlah hasil bagi dan sisanya, jika:
x3 + 7x2 + 4 dibagi (x – 2)
Penyelesaian:
Teknik Biasa

Jadi, hasil baginya H(x) = x2 + 9x + 18 dan sisa S = 40
Teknik Skema/Horner
Pembagian dengan (x – k)
Jika pembagi suatu suku banyak/polinomial ialah (x – k), maka persamaan proteksi sanggup dituliskan sebagai diberikutf(x) = P(x) H(x) + S
atau
f(x) = (x – k) H(x) + S
Dimana f(x) ialah suku banyak, (x – k) ialah pembaginya, H(x) ialah hasil baginya, dan S ialah sisa pertolongannya. Oleh alasannya pembagi P(x) = x – k berderajat satu, maka sisa S maksimum berderajat nol atau berupa suatu konstanta yang tidak memuat variabel. Dari bentuk di atas kita akan mendapat Teorema Sisa 1 diberikut
Teorema Sisa 1
Jika suku banyak f(x) dibagi (x – k), maka sisa pertolongannya ialah S = f(k)
Bukti:
f(x) = (x – k) H(x) + S
f(k) = (k – k) H(x) + S
f(k) = 0 H(x) + S
f(k) = S
Jadi, terbukti S = f(k)
melaluiataubersamaini kata lain kita akan mendapat sisa dari suatu proteksi f(x) dengan pembagi (x – k) dengan mensubstitusi k ke suku banyak f(x)
Untuk memilih hasil bagi dan sekaligus sisa proteksi dari suatu suku banyak kita sanggup memakai dua cara yaitu cara proteksi biasa (cara bersusun) dan cara skema atau horner/skema. Untuk lebih jelasnya perhatikan pola soal diberikut
misal 1
Tentukanlah hasil bagi dan sisanya, jika:
x3 + 7x2 + 4 dibagi (x – 2)
Penyelesaian:
Teknik Biasa

Jadi, hasil baginya H(x) = x2 + 9x + 18 dan sisa S = 40
Teknik Skema/Horner
Jadi, hasil baginya H(x) = x2 + 9x + 18 dan sisa S = 40
melaluiataubersamaini memakai Teorema Sisa 1, kita juga sanggup memilih sisa pertolongannya yaitu:
S = f(x)
S = f(2)
= (2)3 + 7(2)2 + 4
= 8 + 28 + 4
= 40
Pembagian dengan (ax + b)
Pembagian suku banyak f(x) dengan (ax + b), sanggup ditetapkan sebagai diberikut
Nilai S (sisa) sanggup ditetapkan dengan Teorema Sisa 2 diberikut
Teorema Sisa 2
Jika suku banyak f(x) dibagi (ax + b), maka sisa pertolongannya ialah S = f ( -b/a )
Teknik pembuktiannya hampir sama dengan Teorema Sisa 1.
Untuk lebih memahami proteksi suku banyak dengan (ax + b), perhatikan pola diberikut
misal 2
Tentukanlah hasil bagi dan sisanya, kalau 6x3 - 2x2 – x + 7 dibagi (3x + 2)
Penyelesaian:
Untuk menyelesaiakan soal di atas akan dipakai dengan cara horner, untuk cara biasa silahkan anda coba sendiri
Dari cara horner di atas diperoleh H(x) = 6x2 – 6x + 3, sehingga hasil baginya
dan sisa pertolongannya ialah 5
Pembagian dengan (ax2 + bx + c)
Pembagian suku banyak dengan ax2 + bx + c, di mana a ≠ 0 sanggup dilakukan dengan cara biasa apabila ax2 + bx + c tidak sanggup difaktorkan, sedangkan kalau ax2 + bx + c sanggup difaktorkan sanggup dilakukan dengan cara Horner. Dari proteksi dengan ax2 + bx + c ini diperoleh Teorema Sisa 3 yaitu
Teorema Sisa 3
Jika suatu suku banyak f(x) dibagi (x – a)(x – b), maka sisanya ialah S = px + q di mana f(a) = pa + q dan f(b) = pb + q
Dalam hal ini, akan dibahas terkena proteksi dengan cara biasa saja, alasannya lebih praktis dipakai dan diberikut ialah contohnya
misal 3
Tentukanlah hasi bagi dan sisanya, kalau 4x3 + x2 + 2x – 5 dibagi (x2 + 2x – 3)
Penyelesaian
Jadi, hasil baginya 4x - 7 dan sisanya ialah 28x - 26
Berikut ini ialah pola soal lainnya yang berkaitan dengan proteksi suku banyak, yang mungkin akan menambah pemahaman anda terkena proteksi suku banyak
misal 4
Tentukan nilai a sehingga 2x3 + x2 – 13x + a habis dibagi (x – 2), kemudian tentukan hasil baginya
Penyelesaian
Untuk menuntaskan soal di atas kita sanggup memakai Teorema Sisa 1. Karena 2x3 + x2 – 13x + a habis dibagi (x – 2) maka sisanya 0. Kita substitusikan x = 2 pada suku banyak
f(x) = S
f(2) = 0
2(2)3 + 22 – 13(2) + a = 0
16 + 4 - 26 + a = 0
-6 + a = 0
a = 6
Sehingga, suku banyak menjadi 2x3 + x2 – 13x + 6. Untuk memilih hasil baginya kita sanggup memakai cara Horner
Jadi, nilai a ialah 6 dan hasil baginya ialah 2x2 + 5x – 3
misal 5
Tentukanlah nilai a dan b, kalau x3 + ax + b habis dibagi (x2 + x + 1)
Penyelesaian
Karena x3 + ax + b habis dibagi (x2 + x + 1) maka sisanya ialah 0. melaluiataubersamaini memakai proteksi cara biasa diperoleh
Dari, bentuk di atas diperoleh
ax + x = -x
(a + 1)x = -x
a + 1 = -1
a = -2
dan
b = -1
Jadi, nilai a = -2 dan b = -1
Sekian dan biar bermanfaa






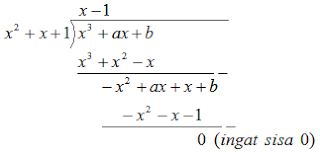
0 Response to "Pembagian Suku Banyak Dan Referensi Soalnya"
Posting Komentar